Wednesday, December 21, 2011
Sunday, December 18, 2011
Monday, December 12, 2011
Wednesday, December 7, 2011
Monday, December 5, 2011
Graphing Trig Functions
I just realized that I never posted notes from 4.5, so they're here too!
PC 4.6 Graphs of Other Trig Functions Notes
PC 4.5 Graphs of Sine and Cosine
PC 4.6 Graphs of Other Trig Functions Notes
PC 4.5 Graphs of Sine and Cosine
Thursday, November 17, 2011
Tuesday, November 15, 2011
Linear and Angular Speed Answers
I did these in a different order than you may have, so watch out! :)
PC 4.1 Linear and Angular Velocity
Thursday, November 10, 2011
Trig stuff
Some trig resources that you may find helpful:
1. Trig Definition Sheet (has unit circle, right triangle trig, domains and ranges)
2. Trig Laws and Identities Sheet (we'll get to these around chapter 5)
3. Khan Academy videos (It's a guy reteaching what we did in class in case you need to see it again)
Another fun way to help you remember your ordered pairs (aka sin and cos values):
PC The Finger Trick for Trig
1. Trig Definition Sheet (has unit circle, right triangle trig, domains and ranges)
2. Trig Laws and Identities Sheet (we'll get to these around chapter 5)
3. Khan Academy videos (It's a guy reteaching what we did in class in case you need to see it again)
Another fun way to help you remember your ordered pairs (aka sin and cos values):
PC The Finger Trick for Trig
Wednesday, November 9, 2011
Monday, November 7, 2011
Friday, November 4, 2011
Thursday, November 3, 2011
Tuesday, November 1, 2011
Ch 3 Review Stuff
Here are the (edited) slides that I showed you in class today...
And the answers to the review worksheet:
PC Ch 3 Review
Ch 3 rev trashketball exp logs
View more presentations from Kristen Fouss
And the answers to the review worksheet:
PC Ch 3 Review
Monday, October 31, 2011
Tuesday, October 25, 2011
Where did logs come from?
The question has come up a few times in the last week or so... where did logs come from? Are natural logs really abbreviated ln because it was the inventor/discoverer's initials?
Here are some resources for you to check out if you're so inclined.
1. History of logs
2. wikipedia entry (which says it wasn't until the next century before a connection was made with exponential functions!)
3. Lots of log stuff
1. History of logs
2. wikipedia entry (which says it wasn't until the next century before a connection was made with exponential functions!)
3. Lots of log stuff
Sunday, October 23, 2011
Tuesday, October 18, 2011
Monday, October 17, 2011
Thursday, October 13, 2011
Friday, October 7, 2011
Wednesday, October 5, 2011
Friday, September 30, 2011
The cubic pattern
In case you're interested (and someone asked for this, so I know you might be!), here's the pattern we discovered today with the cubic polynomial.
Start with a function.
f(x) =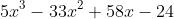
Find the zeros. We picked out 2 and 4 (checked with synthetic division) and ended up with 3/5 as our last.
How can you build the cubic polynomial if you know the zeros (without doing all of the messy binomial multiplication)? Here we go!
Step 1: Factor out the 5. (This only works if the leading coefficient of 1).
=5(x^{3}-\frac{33}{5}x^{2}+\frac{58}{5}x-\frac{24}{5}))
Step 2. Find the product of the zeros.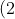(4)\left%20(%20\frac{3}5{}%20\right%20)=\frac{24}{5})
(Which is the opposite of the constant term.)
Step 3. Find the sum of the zeros.
(Which is the opposite of the quadratic term.)
Step 4. Find the sum of the pairwise products which is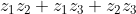 .
.
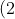(4)+(2)(\frac{5}{3})+(4)(\frac{5}{3})=\frac{58}{5}) (Which is the same as the linear term.)
(Which is the same as the linear term.)
So if you have the zeros of a cubic polynomial with leading coefficient of 1, you can use these patterns to find the polynomial itself. I thought that was pretty cool! (Could you tell? :) )
The next problem was to find a cubic polynomial with zeros at 5, . (It ends up being f(x) =
. (It ends up being f(x) = 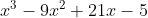 if you're playing along at home.)
if you're playing along at home.)
Start with a function.
f(x) =
Find the zeros. We picked out 2 and 4 (checked with synthetic division) and ended up with 3/5 as our last.
How can you build the cubic polynomial if you know the zeros (without doing all of the messy binomial multiplication)? Here we go!
Step 1: Factor out the 5. (This only works if the leading coefficient of 1).
Step 2. Find the product of the zeros.
(Which is the opposite of the constant term.)
Step 3. Find the sum of the zeros.
(Which is the opposite of the quadratic term.)
Step 4. Find the sum of the pairwise products which is
So if you have the zeros of a cubic polynomial with leading coefficient of 1, you can use these patterns to find the polynomial itself. I thought that was pretty cool! (Could you tell? :) )
The next problem was to find a cubic polynomial with zeros at 5,
Fractals
In case you were totally mesmerized by the Fractal video and would like to see more of it, here's a link.
This is a portion that I think is the coolest - especially the part about the cell phones! (Which we didn't get to in any of your classes :) ).
This is a portion that I think is the coolest - especially the part about the cell phones! (Which we didn't get to in any of your classes :) ).
Watch the full episode. See more NOVA.
Tuesday, September 27, 2011
Friday, September 23, 2011
Thursday, September 22, 2011
Tuesday, September 20, 2011
Monday, September 19, 2011
Tuesday, September 13, 2011
Chapter 1 Review stuff
In the domain for #3, both 3's should have negatives. (-inf, -3) U (-3, 9) U (9, inf)
PC Chapter 1 Review 2011
PC Ch 1 Trashketball
Thursday, September 8, 2011
Wednesday, September 7, 2011
Wednesday, August 31, 2011
Thursday, August 11, 2011
Additional Information
I'd like you all to fill out this survey for me by Friday, August 26th (don't worry - I'll remind you about it in class!). This will take care of the information that teachers normally collect from you the first day.
If you don't know what period you'll be in my class yet, please wait to do the survey until then. I'd like to organize them by classes. If you're just dying to know what period you'll have precalc, email me and I'll let you know. :)
If you don't know what period you'll be in my class yet, please wait to do the survey until then. I'd like to organize them by classes. If you're just dying to know what period you'll have precalc, email me and I'll let you know. :)
Saturday, July 30, 2011
We're nearly there!
I hope you all are having a great summer! If it's anything like mine, it's going waaaaay too quickly.
Here are the answers to the summer work. Please keep in mind that I make dumb mistakes just like everyone else, so if something isn't working out for you, shoot me an e-mail and I'll check it for you.
Please have these problems done and ready to turn in when you come to class the first day! We'll go over any problems that you had and take our quiz on that Friday.
Summer Work Answers
Here are the answers to the summer work. Please keep in mind that I make dumb mistakes just like everyone else, so if something isn't working out for you, shoot me an e-mail and I'll check it for you.
Please have these problems done and ready to turn in when you come to class the first day! We'll go over any problems that you had and take our quiz on that Friday.
Summer Work Answers
Tuesday, May 17, 2011
Thursday, May 12, 2011
11.2 - 3 Review Stuff
The slides from today's game:
11.2 - 3 review slides
The answers to WS 11.2 - 3:
PC WS 11.2 - 3
And a blank copy if you want one:
PC WS 11.2 - 3 blank
11.2 - 3 review slides
The answers to WS 11.2 - 3:
PC WS 11.2 - 3
And a blank copy if you want one:
PC WS 11.2 - 3 blank
Tuesday, May 10, 2011
Thursday, May 5, 2011
11.2 Notes
Day 1: Dividing and Rationalizing Techniques
PC 11.2 Dividing and Rationalizing
Day 2: Using Technology and the Difference Quotient
PC 11.2 Tech and Diff Quot
PC 11.2 Dividing and Rationalizing
Day 2: Using Technology and the Difference Quotient
PC 11.2 Tech and Diff Quot
Tuesday, April 26, 2011
Friday, April 22, 2011
Monday, April 18, 2011
Wednesday, April 13, 2011
Monday, April 11, 2011
Saturday, April 9, 2011
Top Ten Algebra Mistakes
#10. Squaring the negative. A minus a squared unless it’s been snared: 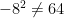
#09. Logarithms: The log of the sum ain’t the sum of the log: 
#08. Shifting function: Add to y go high, add to x go west: 
#07. Inequality: Multiplying the inequality by a negative flips the inequality: 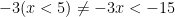
#06. On exponents: When in doubt, write it out: 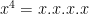
#05. Fractional exponent: Don’t flip over the root. 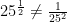
#04. Subtraction: Don’t forget to share the minus and the negativity. 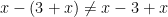
#03. Cancellation: Cancel factors, not individual terms. 
#02. Quadratics: Remember exponents 2, answers 2. 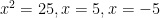
#01. Squaring: Don’t forget to FOIL. 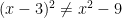 .
.
Thursday, April 7, 2011
Wednesday, April 6, 2011
Monday, April 4, 2011
Monday, March 21, 2011
Tuesday, March 15, 2011
Monday, March 14, 2011
Happy pi day!
I didn't have the chance to show this in class, but it's pretty cool so I wanted you all to see it. :)
Tuesday, March 8, 2011
Thursday, March 3, 2011
9.5 - 6, 6.5 Review Stuff
Slides from today's game (with answers... I think they're all right!)
PC 9.5 - 6, 6.5 game
Answers from WS 9.5 - 6, 6.5
PC WS 9.5 - 6, 6.5
A blank version of the review sheet:
WS 9.5 - 6, 6.5 (blank)
PC 9.5 - 6, 6.5 game
Answers from WS 9.5 - 6, 6.5
PC WS 9.5 - 6, 6.5
A blank version of the review sheet:
WS 9.5 - 6, 6.5 (blank)
Wednesday, March 2, 2011
6.5 Powers and Roots of Complex Numbers in Trig Form
PC 6.5 Powers and Roots
And Multiplying and Dividing from the day before:
PC 6.5 Multiplying and Dividing in Trig Form
And Multiplying and Dividing from the day before:
PC 6.5 Multiplying and Dividing in Trig Form
Subscribe to:
Comments (Atom)

